THE SESQUIPIXEL REMEDY--
| improving digital imaging toward better compression, that data is representing the image desired: Sesquipixel (1.5 squared is 2.25 total) is a specific improvement that firstly smooths and recovers the 'Digital Nyquist Frequency' loss: |
[Topically related to Progressive Image Resolution; Fully Interleaved Scanning; Video Cram (Compression)]
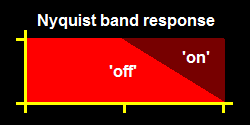
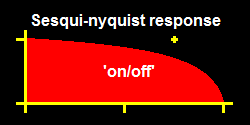
The definition given the Nyquist Frequency Theorem suggests the maximum pass-frequency is half-the-sampling-rate (of a discrete or digital signal system), when in fact said maximum is only at 'on'-registration phase while 'off-' (quadrature) is a washout loss, signals do not get through at such a maximum unless they are 'the-one-signal-of-infinite-length', no 'active-signal' gets through at the Nyquist, and 'signal' at the sub-Nyquist is severely distorted--noticeably in video....
A partial remedy takes all images in double-resolution and computes on-registration and off-registration as alternate-images with equal resolution-- though it still results in double-vision with alternating pixel-widths, breathing, artifacts....
THE SESQUIPIXEL REMEDY--
A better approach slides off-registration a quarter-pixel, thickening pixel lines equally, relatively partially-filling adjacent pixels-- which as a simple 'averaging-mechanism' resolves twice-as-many-thinner-than-double-thicker-than-single-width pixels.
For cgi computer-generated-imagery, a different criterion improves
HDDV by taking vantage of "digital smoothing,"- a specialized concept
better equalizing HDDV to 35mm, its touted film-equivalent, by
spreading each single pixel onto an adjacent pixel, to a "digital
quarter step"; The base value of this method is that the
smoothest-moving line of constant width by adjacent-pixel amplitudes
(1,x) and (x,1), is about x ~ 0.60 (*) ~ 153/255 ... Its
successive offset half steps appear equal, Its apparent line
thickness is roughly a sesquipixel, a half more than single-pixel,
but half-as jumpy or discontinuous "half-moon-jogging," and still
contains a hint of fine-resolution and-motion, and not as smeared
nor 'breathing' as alternately straddling pixels which occur as
the extreme in general pixel sampling....
* (Display Gamma adjusts this, as well as room-brightness, color sensitivities; and vertical and horizontal differ slightly by trace-overlap, and RGB/RGBG pixel placement, yet both are close about the median. Tolerance is apparently tight as unevenness is noticeable at ±10%, in either case: a third, of the web-standard six-cubed 8-bit color-scheme quantum of document-browsers.)
WHEREAS PIXEL WASHOUT--
By comparison on-pixel alignment exhibits alternating thickness
'breathing'; where lines cross one-and-two pixels the half-bright
double-wide lines single-width-equivalently bright about x ~ 0.70
~ 179/255, and fine-detail washout.
(Appraising the two results together, pixel-system-gamma is 2.00, or that is, the original-receptor pixel-system-gamma is 0.50, square root, equivalencing pixels as independent, orthonormalized vectors:-- A "digital box" pixel, uniform, slid to the halfway position, needs 0.50 = 0.71², as in the second result; Slid to the quarter position, needs 0.25/0.75 = 0.58², as in the first result. The 2D sesquipixel roughly equivalences to spreading each original-definition pixel to [0.75 | 0.43 | 0.43 | 0.25], added gamma-correctly to the x-,y-,xy-adjacent pixels; and thence moving fine half-steps horizontally, vertically, diagonally, by column and row alternations.)
[2012 Note on newer flat-panel screens with contrast = 71%, a 136/255 sesquipixel, 162/255 pixelwash, looks almost smoothest: gamma may be 1.0]
Sesquipixel-in-time: Over a pixel-framing-time the pixel turns On, and over the next it turns Off... This gives the pixel a smoother appearance in the case of slow motion, and retains softer alignment in the case of faster motion, (No further time-or-spatial spread would be useful at faster motion: as would only spatially blur...).
(Not referring to a small-child's play....)
When the 'information' is digital but the slope is non-integer, an approximation that fits is itself approximated, and must be recovered....
The 'best' image smoothing will allow for at-most single-hump-overshoot-or-undershoot --without 'ringing' as becomes 'object--ionable' artifacting--
Webpage-image-generation software then-needs support this smoothing by
avoiding representing sharp edges as single-quantum steps.
The 'ideal' bandwidth-constrainted video front-end would have
stacked-3-color pixels atop instantaneous-sum-and-difference
transform-processing and successive-approximation (top-down)
bit-slice compression-transmission, so that-- picture-motion
itself would be realtime, with lossless definition....
Various approximations may suffice technological applications
by quad-adjacent RGBG-pixels (or RGBY), residue-retention at
the compression-transmission level, 3D-and-motion-estimation
at the picture-level (top-pixel-level), pixel-compression by
subdivision-partitioning (rather than omnidirectional), and,
adjacent-value-prediction, etc....
See also treble-thread-gemming.
Another approach, samples 4x8- or 16x16-subpixels in
near-golden-ratio-interleaved order: to be displayed
pointwise-subpixelwise... (4x8 uses 1,3-steps fully correlatively
prime, and 16x16 uses 5,9-steps pushing nearer the middle each step;
golden-ratio ensures that successive steps fill-in with the same
ratio and also tend to fill nearer more-previous points sooner than
the more-preceding).
* (bandwidth-reduced Y-luminance)
** (signal amplitude inversion catches RF spikes as less-noticeable black streaks instead
of white)
High-SNR signal-noise-ratio cable, satellite, DVD, technologies have increased the
potential and actual resolution tenfold, signal levels to 4-5 bits (e.g. QAM16/QAM32),
pixel quantity 8× (esteemed commercial-35mm-film-equivalent, but film has its
own improvements); deriving 6-7 bits from density (dither diminishes as SNR improves,
and is inaccessible in most digital coding schemes * but modulation schemes utilize
the noise reduction for signal-correction robustness).
* (An exception is OQAM64/OQAM128, Offset quad-interstitially compatible to
QAM16/QAM32; cutely called, OQAM's shaver.)
But the technological shift from monotonic amplitude, analog, to digital, required
revised methods of signal error detection-erasure-correction;- Especially digital
signal coding required "smoothing-soothing" of code-errors that would otherwise result
in irreverent, picturally unrelated temporal and spatial optical discompositions
that looked more like TV-"ghosting" patching-in overriding channel discontent than
TV-"snow" or motion aberrations. Simple save remedies involved stalling repeating
the whole prior image or spotwise dark-outs (reduced-brightness image retention).
But ideal smoothing-soothings were something like reduced-spatial-resolution "blur"
and reduced-amplitude-resolution "snow";-- the blur was new and less noticeable than
"snow" as its next image would restore detail. This lead to the selection of the
sum-and-difference transform "blur" and bit-slicing "snow" where the channel could
be bandwidth-truncated (as NTSC is bandwidth-fixed) and signal frames would each
contain the most significant image-bits filled to the allotment.
Ideally also, photons are not pointwise bunched but faster quantum-refreshed, allowing
for 'catching' flicker on the periphery.
(Nevertheless, Because the usual image viewing brightness photon shower is dense and
rapid, pseudorandom works equally well on small scale, spotwise, as for whole images:
An equivalent might then be a prime-ratio interleaving raster-scan in pixel groups,
approximating golden-ratio area-fill, e.g. 7x5-steps in 16x16-blocks ... retaining
some local correlation, a few levels up, and timewise;- and might thus also adapt
high-resolution to lower-bandwidth subsampling and non-microlensed pixelation, camera
and, receiver: present possibility.)
The next-major application of image resolution is in third-dimensional travel, into the
image, as with computer-generated imagery....
; and gave rise to the Haar approach (Haar
Transform, useful as an approach for characterizing common image-source business):
Consider a single pixel of given luminance: Travel into its depth requires
resolving its subpixels. Haar wavelets do this, appending
subdifferences Δx,Δy tilts and ΔΔxy saddle-twist, and
third-dimension Δt and compound double and triple subdifferences, for motion
compression.
Haar is used in astronomy where telescope lens and receptor systems have equal
resolution, adjacent pixels are optically matched and usually spanned by single stars;
But other applications, especially computer-generated imagery, e.g. text/html document
forms, where images are registered to pixel lines, should better differentiate
subpixels directly by the smaller subpixel value and reconstruct the larger
remainder ... we'll designate this, Haar-0 (zero), but a later scheme, switched
compression, shows these are virtually the same.
__
A general note: Expanding an image beyond its pixel-per-pixel resolution, yields an
apparent blocky-digital image, unless the smallest slopes are recalculated ... this may
result in speckly-like performance at edges between slopes. (Also had a similar concern
that could have been improved by smoothing at the single-quantum level: i.e. a difference
of one quantum between adjacent pixels, means specially, they are not, different by one
but the same with a capture-dither that must be smoothed--- a renderer responsibility.)
__
Ideally, original images consist of single photon emitter atoms less than unit-rate each:
A fully parallel nanoprocessor would:
DEEP BACKGROUND (raster-scan video, television committy):
NTSC-defined 4-bit 16-level monochrome reached 7-bit significance with angular density
and temporal noise dither: range, amplitude, smoothing. Color used lower frequency
information in two more bands, Y*-R, Y*-B orthogonal, at the expense of partial
high-frequency
signal in the luminance Y band. And it fit a 6MHz channel, 30 fps × 525 lines
× 760 dx (B&W px; color px; vestigial sideband px; pre-PLL FM sound vx; guard
band xx); Quantization resolution was less noticeably sensitive on the dark end (**).
RESOLUTION:
The nominally ideal video imagery is a faster-than-seen shower of photons averaging to
the original picture scene. Television's raster-scan put up an image-average display,
stiffly similar by lines alternating interleaved; and, cinematograph's shuttering
put up an array of near-simultaneous flashes; both with noticeable flicker, despite
television's energy retention at individual pixels (that gave vidicon cameras
streaking). An ideal digital-time image would put up pixels
in a "pseudorandom" pattern; however, disparate pixel-addressing has little correlation
among adjacent samples,- which correlation would be used arithmetically, simply to
estimate neighbor pixels, non adjacent when jumped. Consequently the advancing
television technology reverted to cinematograph-like framed "progressive scan",--
though computationally only a large frame-memory is needed to nearly reproduce one
from the other.
COMPRESSION:
Localized video-differentiation is highly efficient because objects have local features,
but integration on partial-data and broadcast-noise is unsatisfactory, needs be
locally restabilized to keep integration on-path, and is essentially two-dimensional,-
which last means it must go right to code. Most improvement schemes do progressive
imaging lowpass "subbanding" followed by highpass detailing. Early schemes tried to
be NTSC-compatible by stuffing digital data into the lower-order bits as
analog-tending-digital-codes, "gray snow", half-quantum-offset keying doubling NTSC
spec. 16-level ... tending invisible to analog. In full digital non analog-compatible,
the Haar transform is progressive on closed pixels, -replacing full summation
computations with over-pixel differentials till all coefficients are differentials,
and so pyramidally restabilizing each sub-quad ... Haar remains accurate
to register adjacent edges between quads while SPIHT performs top-down
successive-approximation.
It is of interest to note that the base representation of a count of photons, is itself a
first-level signal reduction, essentially runlength: the total number of values possible
then fits into the arithmetic coding, which I showed was efficiently coded by entropic
choreonumeration,- which can be as arithmetic or not, as
needed. SPIHT typically uses a Huffman coding.
along lines temporally developed from "learned" linear motions